선형대수_01) 선형방정식을 표현하는 세가지 방법

 

선형방정식을 표현하는 세 가지 방법

 

1. Row picture
2. Column picture
3. Matrix form

 

 

1. Row picture

 

• 수평 관점
• 방정식의 나열 하는 방법
• 방정식을 만족하는 모든 지점을 그래프 위에 표시했을 때 그래프가 만나는 지점(방정식을 동시에 만족하는 점) => 해

 

\begin{cases}
    2x+y &=0\\-x+2y &=-3
\end{cases}

 

• 그래프

 

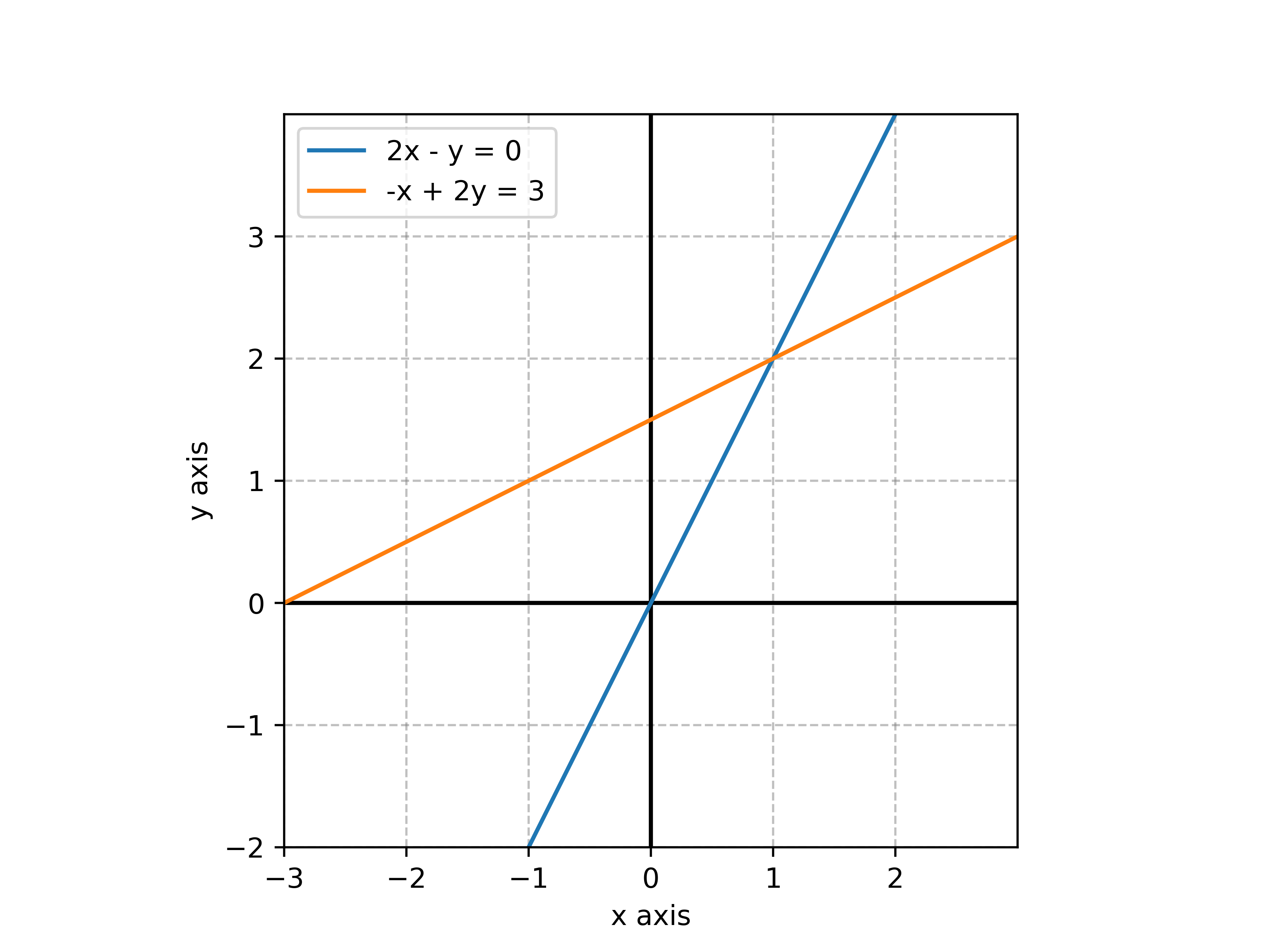
• 그래프 코드

https://github.com/dpcalfola/study_matplotlib/blob/main/linear_algebra_study/linear_algebra_01/equation_01.py

 

 

 

 

 

2. Column picture (중요!)

 

• 수직 관점
• Linear combination of the colemns
• 열 혹은 벡터의 선형 조합
• 방정식을 만족하는 선형 조합 => 해

 

\begin{align}
    x
    \begin{bmatrix}
        2\\-1
    \end{bmatrix}
    +y
    \begin{bmatrix}
        2\\-1
    \end{bmatrix}
    =
    \begin{bmatrix}
        0\\3
    \end{bmatrix}
\end{align}

 

• 그래프

 

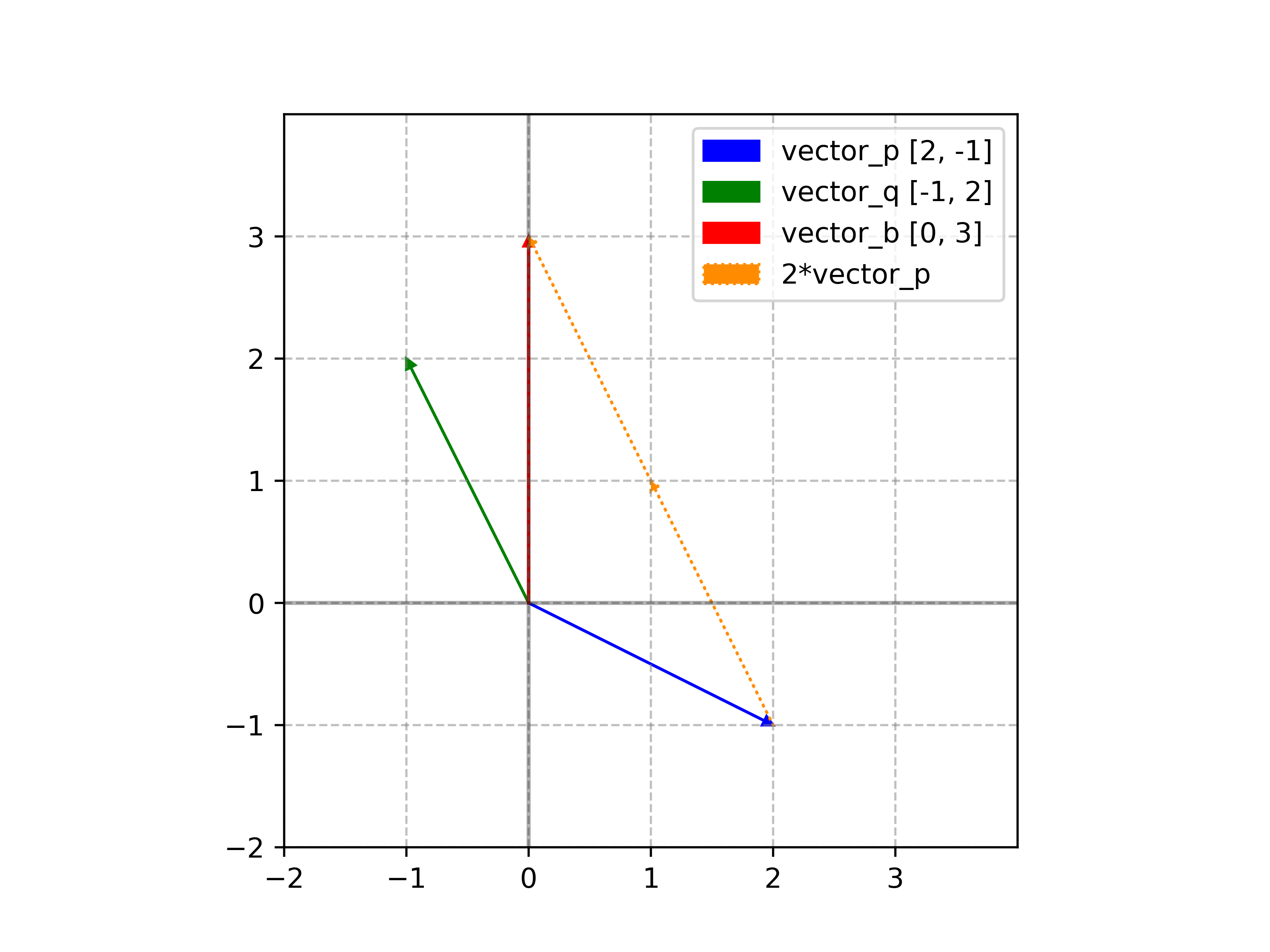
• 그래프 코드

https://github.com/dpcalfola/study_matplotlib/blob/main/linear_algebra_study/linear_algebra_01/vector_01.py

(그래프)

https://github.com/dpcalfola/study_matplotlib/blob/main/linear_algebra_study/classes_and_functions/vector_class.py

(class Vector)

 

 

 

3. Matrix form

 

• 선형대수의 관점
• \( Ax=b\) 형태로 표현
• \( Ax=b\) 모든 b에 대해 해 x를 구할 수 있는가? == columns의 선형 조합이 모든 공간을 채우고 있는가?

 

\begin{align}
    \begin{bmatrix}
        2& -1\\-1& 2
    \end{bmatrix}
    \begin{bmatrix}
        x\\y
    \end{bmatrix}
    =
    \begin{bmatrix}
        0\\3
    \end{bmatrix}
\end{align}

 

 

 

 

Reference

MIT 18.06SC Linear Algebra, Fall 2011

https://youtu.be/J7DzL2_Na80